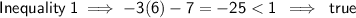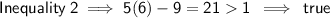Question

Find two solutions to the following system of inequalities. Please write it in ordered pair form.

Answer 1

(5, 5) and (6, 1)

Explanation:

Solutions to the system of inequalities are any points that are in the overlapped shaded region.

For example (5, 5) and (6, 1)

Proof

Find the equations of the two lines.

Blue line

Two points on the line: (-5, 8) and (0, -7)

`\implies \sf slope\:(m)=(change\:in\:y)/(change\:in\:x)=(-7-8)/(0-(-5))=-3`

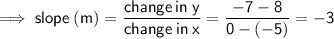
Point-slope form of linear equation:
`\sf y-y_1=m(x-x_1)`

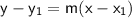
(where m is the slope and (x₁, y₁) is a point on the line)

`\implies \sf y-(-7)=-3(x-0)`

`\implies \sf y=-3x-7`

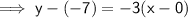
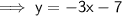
As the shading is above the line, and the line is dashed:

`\sf y > -3x-7`

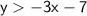
Red line

Two points on the line: (0, -9) and (2, 1)

`\implies \sf slope\:(m)=(change\:in\:y)/(change\:in\:x)=(1-(-9))/(2-0)=5`

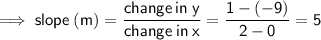
Point-slope form of linear equation:
`\sf y-y_1=m(x-x_1)`

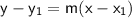
(where m is the slope and (x₁, y₁) is a point on the line)

`\implies \sf y-(-9)=5(x-0)`

`\implies \sf y=5x-9`

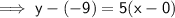
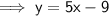
As the shading is below the line, and the line is solid:

`\sf y\leq 5x-9`

`\sf Inequality\:1: y > -3x-7`

`\sf Inequality\:2:y\leq 5x-9`

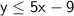
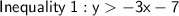
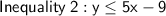
Point (5, 5)

`\sf Inequality\:1\implies -3(5)-7=-22 < 5\: \implies\:true`

`\sf Inequality\:2\implies 5(5)-9=16 > 5\: \implies\:true`

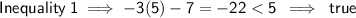
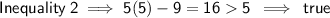
Point (6, 1)

`\sf Inequality\:1\implies -3(6)-7=-25 < 1\: \implies\:true`

`\sf Inequality\:2\implies 5(6)-9=21 > 1\: \implies\:true`