Answer:
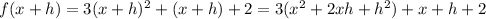
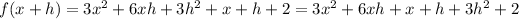
And replacing we got:
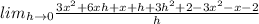
And if we simplfy we got:
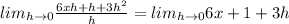
And replacing we got:
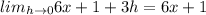
And the bet option would be:
C. 6x + 1
Explanation:
We have the following function given:
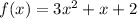
And we want to find this limit:
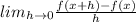
We can begin finding:
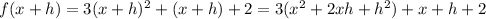
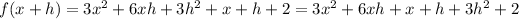
And replacing we got:
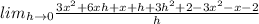
And if we simplfy we got:
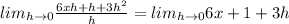
And replacing we got:
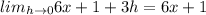
And the bet option would be:
C. 6x + 1