Question

Consider a circle whose equation is x2 + y2 + 4x - 6y - 36 = 0. Which statements are true? Check all that appl"

To begin converting the equation to standard form, subtract 36 from both sides.
mu To complete the square for the x terms, add 4 to both sides.

Answer 1

To complete the square for the x terms, add 4 to both sides.

To convert the given equation of the circle to standard form we should do as follows.

1. Add 36 to both sides of the equation.

`x^(2) +y^(2)+4x-6y-36+36=36\\ x^(2) +y^(2)+4x-6y=36`

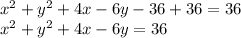
2. We order the terms according to their variables.

`x^(2) +4x +y^(2)-6y=36`

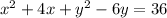
3. Divide the linear term by 2, then elevate it to the square power.

`x^(2) +4x + ((4)/(2) )^(2) +y^(2) -6y+((6)/(2) )^(2) =36`

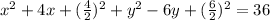
4. Solve operations, and add the same units to the other side of the equation.

`x^(2) +4x+4+y^(2) -6y+9=36+4+9\\`

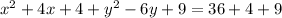
5. Now, we sum costant terms, and factor both trinomials.

`(x+2)^(2) +(y-3)^(2) =49`

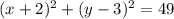
As you can observe, the circle has center at (-2,3) and it has a radius of 7 units.

Notice that the second choice is correct, because we added 4 units to both sides to complete the square for the x terms.