Question

Consider this reaction:

2Cl2O5 —> 2Cl2 + 5O2

At a certain temperature it obeys this rate law.
rate = (2.7.M^-1•s^-1) [Cl2O5]^2

Suppose a vessel contains Cl2O5 at a concentration of 0.600M. calculate how long it takes for the concentration of Cl2O5 to decrease by 94%. you may assume no other reaction is important. round your answer to two digits

Answer 1

`t=9.7s`

Step-by-step explanation:

Hello,

In this case, we have a second order kinetics given the second power of the concentration of chlorine (V) oxide in the rate expression, thus, the integrated equation for the concentration decay is:

`(1)/([Cl_2O_5])=kt+(1)/([Cl_2O_5]_0)`

Thus, the final concentration for a 94% decrease is:

`[Cl_2O_5]=0.600M-0.600M*0.94=0.036M`

Therefore, we compute the time for such decrease:

`kt=(1)/([Cl_2O_5])-(1)/([Cl_2O_5]_0)=(1)/(0.036M)-(1)/(0.60M) =26.1M^(-1)`

`t=(26.1M^(-1))/(k)= (26.1M^(-1))/(2.7M^(-1)*s^(-1))\\\\t=9.7s`

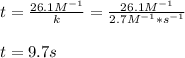
Regards.