Answer:

Explanation:
Step 1: Identify the approach:
With this problem, the general solution is to try manipulate given data and transform data into a new form, in which, the desired value
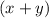 is on the left side and all of other components which do not contain
is on the left side and all of other components which do not contain
 or
or
 are on the right side.
are on the right side.
Step 2: Analyze:
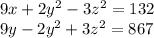
Realize that in both equations, the
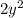 and
and
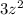 are in form of different signs. Then adding up corresponding sides of both equation can help eliminate these undesired components.
are in form of different signs. Then adding up corresponding sides of both equation can help eliminate these undesired components.
Step 3: Perform manipulation:

Rearrange:
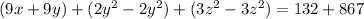
Simplify:
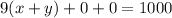
Simplify:

Hope this helps!
:)