Answer:
Approximately
 (assuming that
(assuming that
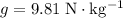 .)
.)
Step-by-step explanation:
The question provided very little information about this motion. Therefore, replace these quantities with letters. These unknown quantities should not appear in the conclusion if this question is actually solvable.
- Let
 represent the mass of this car.
represent the mass of this car. - Let
 represent the radius of the circular track.
represent the radius of the circular track.
This answer will approach this question in two steps:
- Step one: determine the centripetal force when the car is about to skid.
- Step two: calculate the coefficient of static friction.
For simplicity, let
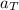 represent the tangential acceleration (
represent the tangential acceleration (
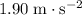 ) of this car.
) of this car.
Centripetal Force when the car is about to skid
The question gave no information about the distance that the car has travelled before it skidded. However, information about the angular displacement is indeed available: the car travelled (without skidding) one-quarter of a circle, which corresponds to
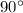 or
or
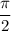 radians.
radians.
The angular acceleration of this car can be found as
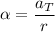 . (
. (
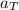 is the tangential acceleration of the car, and
is the tangential acceleration of the car, and
 is the radius of this circular track.)
is the radius of this circular track.)
Consider the SUVAT equation that relates initial and final (tangential) velocity (
 and
and
 ) to (tangential) acceleration
) to (tangential) acceleration
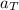 and displacement
and displacement
 :
:
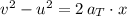 .
.
The idea is to solve for the final angular velocity using the angular analogy of that equation:
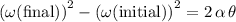 .
.
In this equation,
 represents angular displacement. For this motion in particular:
represents angular displacement. For this motion in particular:
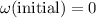 since the car was initially not moving.
since the car was initially not moving.
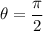 since the car travelled one-quarter of the circle.
since the car travelled one-quarter of the circle.
Solve this equation for
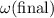 in terms of
in terms of
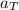 and
and
 :
:
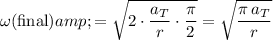 .
.
Let
 represent the mass of this car. The centripetal force at this moment would be:
represent the mass of this car. The centripetal force at this moment would be:
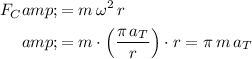 .
.
Coefficient of static friction between the car and the track
Since the track is flat (not banked,) the only force on the car in the horizontal direction would be the static friction between the tires and the track. Also, the size of the normal force on the car should be equal to its weight,
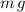 .
.
Note that even if the size of the normal force does not change, the size of the static friction between the surfaces can vary. However, when the car is just about to skid, the centripetal force at that very moment should be equal to the maximum static friction between these surfaces. It is the largest-possible static friction that depends on the coefficient of static friction.
Let
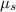 denote the coefficient of static friction. The size of the largest-possible static friction between the car and the track would be:
denote the coefficient of static friction. The size of the largest-possible static friction between the car and the track would be:
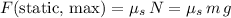 .
.
The size of this force should be equal to that of the centripetal force when the car is about to skid:
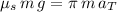 .
.
Solve this equation for
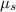 :
:
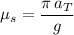 .
.
Indeed, the expression for
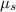 does not include any unknown letter. Let
does not include any unknown letter. Let
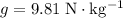 . Evaluate this expression for
. Evaluate this expression for
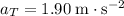 :
:
 .
.
(Three significant figures.)