Question

1. How many solutions does the following equation have?

2x2 – 3x + 5 = 2x2.*- 3x + 5
no solution
- 2x -2% -2X
O
o -5% +5=0
2. Use the quadratic formula to solve the equation. If necessary, round to the nearest
hundredth.
x2 + 3 = -4x+3=- 4x
3- 4x
3. Solve the equation using the Zero-Product Property,
4p(5p+ 10) = 0
20p²+40p=0
-20p^2-20p^2
I just want to know if I got it right?

​

Answer 1

1. The equation has no real solutions

2.
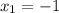`x_1 = -1` and
`x_2 = -3`

3. p = 0 and p = -2

Explanation:

1. Eq: x² - 3x + 5

discriminant: b² - 4(a)(c) = (-3)² - 4(1)(5) = 9 - 20 = -19 < 0

Therefore, the equation has no real solutions

2. Eq: x² + 3 = -4x

0 = x² + 4x + 3

`x = (-b \pm √(b^2 - 4(a)(c)))/(2(a))`

`x = (-4 \pm √(4^2 - 4(1)(3)))/(2(1))`

`x = (-4 \pm 2)/(2)`

`x_1 = (-4 + 2)/(2)`

`x_1 = -1`

`x_2 = (-4 - 2)/(2)`

`x_2 = -3`

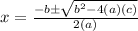
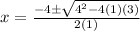
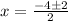
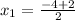
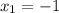
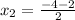
3. Eq: 4p(5p+ 10) = 0

Zero-Product Property states that:

4p = 0 or 5p + 10 = 0

The first solution is p = 0. The second is:

5p + 10 = 0

5p = -10

p= -10/5 = -2