Question

A market research firm supplies manufacturers with estimates of the retail sales of their products from samples of retail stores. Marketing managers are prone to look at the estimate and ignore sampling error. A random sample of 36 stores this year shows mean sales of 53 units of a small appliance with a standard deviation of 12 units. During the same point in time last year, a random sample of 49 stores had mean sales of 41 units with standard deviation 6 units.

It is of interest to construct a 95 percent confidence interval for the difference in population means ?1??2, where ?1 is the mean of this year's sales and ?2 is the mean of last year's sales.

Enter values below rounded to three decimal places.

(a) The estimate is: _________ .

(b) The standard error is: ____________________ .

Answer 1

The 95% confidence interval for the difference of means is (7.67, 16.33).

The estimate is Md = 12.

The standard error is sM_d = 2.176.

Explanation:

We have to calculate a 95% confidence interval for the difference between means.

The sample 1 (this year's sales), of size n1=36 has a mean of 53 and a standard deviation of 12.

The sample 2 (last year's sales), of size n2=49 has a mean of 41 and a standard deviation of 6.

The difference between sample means is Md=12.

`M_d=M_1-M_2=53-41=12`

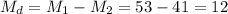
The estimated standard error of the difference between means is computed using the formula:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(12^2)/(36)+(6^2)/(49)}\\\\\\s_(M_d)=√(4+0.735)=√(4.735)=2.176`

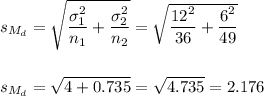
The degrees of freedom are:

`df=n_1+n_2-1=36+49-2=83`

The critical t-value for a 95% confidence interval and 83 degrees of fredom is t=1.989.

The margin of error (MOE) can be calculated as:

`MOE=t \cdot s_(M_d)=1.989 \cdot 2.176=4.328`

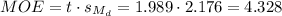
Then, the lower and upper bounds of the confidence interval are:

`LL=M_d-t \cdot s_(M_d) = 12-4.328=7.67\\\\UL=M_d+t \cdot s_(M_d) = 12+4.328=16.33`

The 95% confidence interval for the difference of means is (7.67, 16.33).