Question

The interior angles of a triangle are 60,45and 75.the shortest side is 10cm less than the longest side, determine the perimeter of the triangle to the nearest cm.include a diagram please and thank you!!

Answer 1

20 cm.

Explanation:

We know that the permiter is defined as

`P=L+S+M`

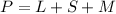
Where
`L` is the longest side,
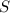`S` is the smallest and
`M` is the middle side.

If
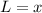`L=x` then,
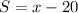`S=x-20`, where we need to find an expression for
`M` using the law of cosines.

`M^(2) =L^(2)+S^(2)-2 * L * S * cos(60\°)\\M=\sqrt{x^(2)+(x-20)^(2)-x(x-20)}\\M=\sqrt{x^(2) +x^(2)-40x+400-x^(2)+20x}=\sqrt{x^(2)-20x+400}`

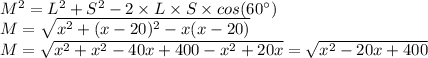
Replacing all expression, the perimeter is

`P=x+x-20+\sqrt{x^(2)-20x+400}\\P=2x-20+\sqrt{x^(2)-20x+400}`

Using a calculator, the perimeter is 20 units centimeters.