Question

As part of an insurance company’s training program, participants learn how to conduct an analysis of clients’ insurability. The goal is to have participants achieve a time in the range of 30 to 47 minutes. Test results for three participants were: Armand, a mean of 37.0 minutes and a standard deviation of 3.0 minutes; Jerry, a mean of 38.0 minutes and a standard deviation of 2.0 minutes; and Melissa, a mean of 38.5 minutes and a standard deviation of 2.9 minutes.

a.Which of the participants would you judge to be capable? (Do not round intermediate calculations. Round your answers to 2 decimal places.)

Participants :

Armand: Cpk _____ Cp Capable ? No/Yes

Jerry: Cpk _____ Capable ? Yes/No

Melissa Cp ________ No/Yes

b.Can the value of the Cpk exceed the value of Cp for a given participant?

yes or no

Answer 1

1) cpk < 1.33, therefore it is not capable

b) cpk = 1.33, therefore it is capable

c) cpk < 1.33, therefore it is not capable

2) Cpk can never be greater than the Cp, but can be equal to it

Explanation:

Upper limit (USL) = 47 minutes and Lower limit (LSL) = 30 minutes

1)

a) mean (μ) = 37 minutes, standard deviation (σ) = 3 minutes

`cpk=min((USL-\mu)/(3\sigma), (\mu - LSL)/(3\sigma))=min((47-37)/(3*3),(37-30)/(3*3) )=min(1.11,0.78)=0.78`

`cp=((USL-LSL)/(6\sigma))=(47-30)/(6*3)=0.94`

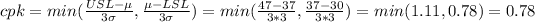
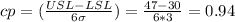
cpk < 1.33, therefore it is not capable

b) mean (μ) = 38 minutes, standard deviation (σ) = 2 minutes

`cpk=min((USL-\mu)/(3\sigma), (\mu - LSL)/(3\sigma))=min((47-38)/(3*2),(38-30)/(3*2) )=min(1.5,1.33)=1.33`

`cp=((USL-LSL)/(6\sigma))=(47-30)/(6*2)=1.42`

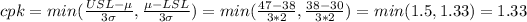
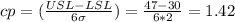
cpk = 1.33, therefore it is capable

c) a) mean (μ) = 38.5 minutes, standard deviation (σ) = 2.9 minutes

`cpk=min((USL-\mu)/(3\sigma), (\mu - LSL)/(3\sigma))=min((47-38.5)/(3*2.9),(38.5-30)/(3*2.9) )=min(0.98,0.98)=0.98`

`cp=((USL-LSL)/(6\sigma))=(47-30)/(6*2.9)=0.98`

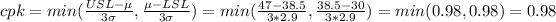
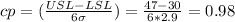
cpk < 1.33, therefore it is not capable

2) Cpk can never be greater than the Cp, but can be equal to it