Question

Assume that the heights of men are normally distributed with a mean of 70.9 inches and a standard deviation of 2.1 inches. If 36 men are randomly selected, find the probability that they have a mean height greater than 71.9 inches. Round to four decimal places.

Answer 1

The probability that they have a mean height greater than 71.9 inches

P( x⁻ ≥71.9) = 0.0022

Explanation:

Explanation:-

Given mean of the Population μ= 70.9

Standard deviation of the Populationσ = 2.1

Given sample size 'n' =36

let x⁻ be the mean height

given x⁻ =71.9 inches

`Z=(x^(-) -mean)/((S.D)/(√(n) ) )`

`Z=(71.9 -70.9)/((2.1)/(√(36) ) ) = (1)/(0.35) = 2.85`

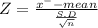
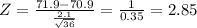
The probability that they have a mean height greater than 71.9 inches

P( x⁻ ≥71.9) = P(Z ≥ 2.85)

= 1 - P(Z≤ 2.85)

= 1 - ( 0.5 + A(2.85)

= 0.5 - A( 2.85)

= 0.5 - 0.4978

= 0.0022

The probability that they have a mean height greater than 71.9 inches

P( x⁻ ≥71.9) = 0.0022