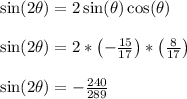Answer:
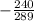
=========================================================
Step-by-step explanation:
Use the pythagorean trig identity
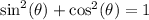 and plug in the fact that
and plug in the fact that
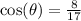
Isolating sine leads to
 . I'm skipping the steps here, but let me know if you need to see them.
. I'm skipping the steps here, but let me know if you need to see them.
The result is negative because we're in quadrant 4, when y < 0 so it's when sine is negative.
Therefore,