Question

John averages 58 words per minute on a typing test with a standard deviation of 11 words per minute. Suppose John's words per minute on a minute on a typing test. Then X~N(58,11)

Answer 1

The z score when x =72 is:

`z = (72-58)/(11)= 1.273`

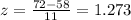
The mean is 58

This z-score tells you that x= 72 is 1.273 standard deviations to the right of the mearn.

Explanation:

Assuming the following info for the question: Suppose John's words per minute on a typing test are normally distributed. Let X -the number of words per minute on a typing test. Then X N(58, 11) If necessary, round to three decimal places.

Provide your answer below rds per minute in a typing test on Sunday. The z score when x =72 is

For this case we know that the variable of interest is modelled with the normal distribution:

`X \sim N (\mu= 58, \sigma=11)`

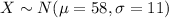
And the z score is given by:

`z = (X -\mu)/(\sigma)`

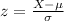
And replacing we got:

`z = (72-58)/(11)= 1.273`

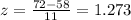
The mean is 58

This z-score tells you that x= 72 is 1.273 standard deviations to the right of the mearn.