Answer:
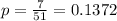
And then the probability that is NOT from sport temas using the complement rule is given by:
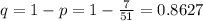
And if we convert that into % we got:

Approximately 86.27% of the floats were NOT sports teams
Explanation:
For this case we can begin finding the % of floats that were from sport tems using the Laplace definition of probability given by:
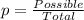
And replacing we got:
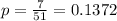
And then the probability that is NOT from sport temas using the complement rule is given by:
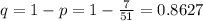
And if we convert that into % we got:

Approximately 86.27% of the floats were NOT sports teams