Question

An 80-kg quarterback jumps straight up in the air right before throwing a 0.43-kg football horizontally at 15 m/s . How fast will he be moving backward just after releasing the ball?

Sort the following quantities as known or unknown. Take the horizontal direction to be along the x axis.

mQ: the mass of the quarterback
mB: the mass of the football
(vQx)i: the horizontal velocity of quarterback before throwing the ball
(vBx)i: the horizontal velocity of football before being thrown
(vQx)f: the horizontal velocity of quarterback after throwing the ball
(vBx)f: the horizontal velocity of football after being thrown

Answer 1

vBxf = 0.08625m/s

Step-by-step explanation:

This is a problem about the momentum conservation law. The total momentum before equals the total momentum after.

`p_f=p_i`

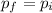
pf: final momentum

pi: initial momentum

The analysis of the momentum conservation is about a horizontal momentum (x axis). When the quarterback jumps straight up, his horizontal momentum is zero. Then, after the quarterback throw the ball the sum of the momentum of both quarterback and ball must be zero.

Then, you have:

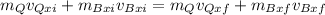`m_Qv_(Qxi)+m_(Bxi)v_(Bxi)=m_Qv_(Qxf)+m_(Bxf)v_(Bxf)` (1)

mQ: the mass of the quarterback = 80kg

mB: the mass of the football = 0.43kg

(vQx)i: the horizontal velocity of quarterback before throwing the ball = 0m/s

(vBx)i: the horizontal velocity of football before being thrown = 0m/s

(vQx)f: the horizontal velocity of quarterback after throwing the ball = ?

(vBx)f: the horizontal velocity of football after being thrown = 15 m/s

You replace the values of the variables in the equation (1), and you solve for (vBx)f:

`0\ kgm/s=-(80kg)(v_(Bxf))+(0.46kg)(15m/s)\\\\v_(Bxf)=((0.46kg)(15m/s))/(80kg)=0.08625(m)/(s)`

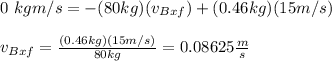
Where you have taken the speed of the quarterback as negative because is in the negative direction of the x axis.

Hence, the speed of the quarterback after he throws the ball is 0.08625m/s