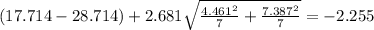Answer:

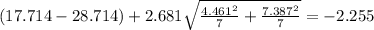
Explanation:
For this case we have the following info given:
Treatment: 12 13 15 19 20 21 24
Control: 18 23 24 30 32 35 39
We can find the sample mean and deviations with the the following formulas:

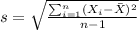
And repaplacing we got:
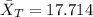 the sample mean for treatment
the sample mean for treatment
 the sample mean for treatment
the sample mean for treatment
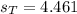 the sample deviation for treatment
the sample deviation for treatment
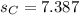 the sample deviation for control
the sample deviation for control
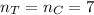 the sample size for each sample
the sample size for each sample
The degrees of freedom are given by:
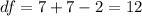
The confidence interval for the difference of means is given by:
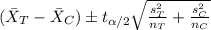
The confidence is 98% so then the significance is
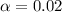 and
and
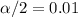 . Then the critical value would be:
. Then the critical value would be:
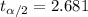
And replacing we got: