The area of a circle is 18 pi square inches. If the area of a sector of this circle is 6 pi square inches, then which of the following must be the sector's central angle?

Question

asked Dec 22, 2021 87.7k views

1 Answer

Katisha · Answer 1 · 2021-12-26T03:37:59+0000

Answer:

Explanation:

Area of a sector =
$(\theta)/(360) * \pi r^(2)\ where\ \pi r^(2) \ is\ the\ area\ of\ the\ circle$

theta is the sector's central angle

Area of the sector =
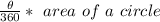
$(\theta)/(360) * \ area\ of\ a\ circle$

Given area of a circle = 18πin² and area of a sector = 6πin²

On substituting;

6π =
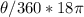
$\theta/360 * 18 \pi$

Dividing both sides by 18π we have;

1/3 =
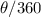
$\theta/360$

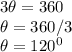
$3 \theta = 360\\\theta = 360/3\\\theta = 120^(0)$

The sector's central angle is 120°