
To find :-
The value of x in the angles of Pentagon
Given :-
Here we have been provided 5 angles in Pentagon
x°, (x - 44)°, (x + 6)°, 125°, and 117°
Solution :-
We will find the value of x with the angle sum property.
Now, we will find the sum of angles of Pentagon
there is a formula
(n - 2) × 180°
n = no. of sides of above shape
here n = 5
(5 - 2) × 180°
3 × 180° = 540°
Now will add the above given angle in the diagram and put equal to 540°.
x° + (x - 44)° + (x + 6)° + 125° + 117° = 540° (angle sum property)
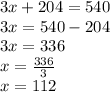
x = 112°
further we will find further 2 angles related to x.
x - 44 = 112 - 44 = 68°
x + 6 = 112 + 6 = 118°
Result :-
The all angles of Pentagon are
125°, 117°, 118°, 112°, and 68°.