Question

Lebron James and Stephen Curry are playing an intense game of minigolf. The final(18th) hole is 8.2 m away from the tee box (starting location) at an angle of 20◦ east of north. Lebron’s first shot lands 8.6 m away at an angle of 35.2◦ east of north and Steph’s first shot lands 6.1 m away at an angle of 20◦ east of north. Assume that the minigolf course is flat.

(A) Which ball lands closer to the hole?
(B) Each player sunk the ball on the second shot. At what angle did each player hit their ball to reach the hole?

Answer 1

A. we will see that the notion
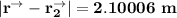`\mathbf` which denotes Stephen Curry illustrates that Stephen Curry minigolf ball shot is closer

B. Lebron James hits at an angle of 17.48° North -East.

The direction of Stephen is = 20° due to East of North

Step-by-step explanation:

Let
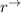`r ^ {\to` represent the position vector of the hole;

Also; using the origin as starting point. Let the east direction be along the positive x axis and the North direction be + y axis

Thus:

`r ^ {\to` =
`8.2 \ sin 20^0 \hat i + 8.2 \ cos 20 \hat j`

`r ^ {\to` =
`(2.8046 \hat i + 7.7055 \hat j ) m`

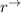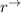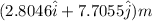
Let
`r_1 ^ \to` be the position vector for Lebron James's first shot

So;

`r_1 ^ \to` =
`(8.6 \ sin \ 35.2 )^0 \hat i + 8.6 \ cos \ ( 35.2)^0 \hat j`

`r^ \to = (4.9573 \hat i + 7.02745 \hat j) m`

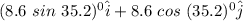
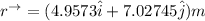
Let
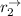`r_2 ^ \to` be the position vector for Stephen Curry's shot

`r_2 ^ \to`
`=6.1 \ sin 20^0 \hat i + 6.1 \ cos \ 20 \hat j`

`r_2 ^ \to` =
`(2.0863 \hat i + 5.7321 \hat j )m`

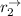
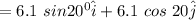
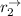However;

`r ^ \to - r_1 ^\to = (-2.1527 \hat i + 0.67805 \hat j) m`

`\mathbf`

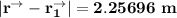
Also;

`r ^ \to - r_2 ^\to = (0.71013 \hat i - 1.9734 \hat j) m`

`\mathbf`

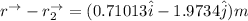
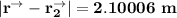
Thus; from above ; we will see that the notion
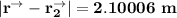`\mathbf = 2.10006 \ m` which denotes Stephen Curry illustrates that Stephen Curry minigolf ball shot is closer

B .

For Lebron James ;

The angle can be determine using the trigonometric function:

`tan \theta = ( (0.67805)/(-2.1527)) \\ \\ tan \theta = -0.131498 \\ \\ \theta = tan ^(-1) ( -0.31498) \\ \\ \mathbf{\theta = -17.48^0}`

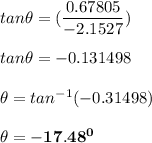
Thus Lebron James hits at an angle of 17.48° North -East.

For Stephen Curry;

`tan \theta = ( (-1.9734)/(0.7183)) \\ \\ tan \theta = -2.74732 \\ \\ \theta = tan ^(-1) ( -2.74732) \\ \\ \mathbf{\theta = -70.0^0}`

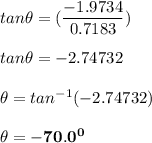
The direction of Stephen is = 90° - 70° = 20° due to East of North