Answer:
a). Area = 54 square units
b). Perimeter = 33.7 units
Explanation:
Vertices of the triangle ABC are A(-4, -2), B(1, 7) and C(8, -2).
(a). Area of the triangle ABC =
![(1)/(2)[x_(1)(y_(2)-y_(3))+x_(2)(y_(3)-y_(1))+x_(3)(y_(1)-y_(2))]](https://img.qammunity.org/2021/formulas/mathematics/high-school/lm38ur8s8ludble4lqaz92wwk1sejwdxuc.png) (Absolute value)
(Absolute value)
By substituting the values from the given vertices,
Area =
![(1)/(2)[(-4)(7+2)+(1)(-2+2)+8(-2-7)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/1i7munkk8j32njngyehiu49dru878vdy2t.png)
=
![(1)/(2)[-36+0-72]](https://img.qammunity.org/2021/formulas/mathematics/high-school/yum7l9l1tvhjl8yshm46wcvl5z1xvwpape.png)
=
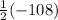
= (-54) unit²
Therefore, absolute value of the area = 54 square units
(b). Distance between two vertices (a, b) and (c, d)
d =
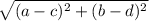
AB =

=

= 10.295 units
BC =
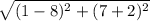
=

= 11.402 units
AC =
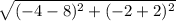
= 12 units
Perimeter of the triangle = AB + BC + AC = 10.295 + 11.402 + 12
= 33.697
≈ 33.7 units