Question

part 3. Find the value of the trig function indicated, use Pythagorean theorem to find the third side if you need it.​

Answer 1

Answer:
`\bold{9)\ \sin \theta=(1)/(3)\qquad 10)\ \sin \theta = (4)/(5)\qquad 11)\ \cos \theta = (√(11))/(6)\qquad 12)\ \tan \theta = (17\sqrt2)/(26)}`

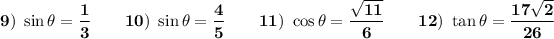
Explanation:

Pythagorean Theorem is: a² + b² = c² , where "c" is the hypotenuse

`9)\ \sin \theta=\frac{\text{side opposite of}\ \theta}{\text{hypotenuse of triangle}}=(4)/(12)\quad \rightarrow \large\boxed{(1)/(3)}`

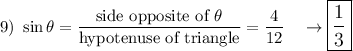
Note: 4² + (8√2)² = hypotenuse² → hypotenuse = 12

`10)\ \sin \theta=\frac{\text{side opposite of}\ \theta}{\text{hypotenuse of triangle}}=(16)/(20)\quad \rightarrow \large\boxed{(4)/(5)}`

Note: 12² + opposite² = 20² → opposite = 16

`11)\ \cos \theta=\frac{\text{side adjacent to}\ \theta}{\text{hypotenuse of triangle}}=(√(11))/(6)\quad =\large\boxed{(√(11))/(6)}`

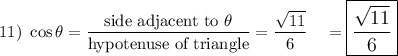
Note: adjacent² + 5² = 6² → adjacent = √11

`12)\ \tan \theta=\frac{\text{side opposite of}\ \theta}{\text{side adjacent to}\ \theta}=(17)/(13\sqrt2)\quad =\large\boxed{(17\sqrt2)/(26)}`

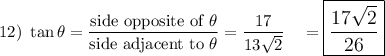
Note: adjacent² + 7² = (13√2)² → adjacent = 17