Answer:
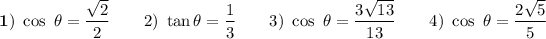
Explanation:
Pythagorean Theorem is: a² + b² = c², where "c" is the hypotenuse
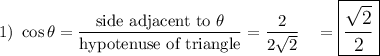
Note: 2² + 2² = hypotenuse² → hypotenuse = 2√2
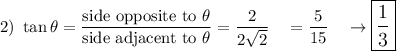
Note: hypotenuse not needed for tan θ
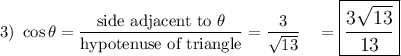
Note: 2² + 3² = hypotenuse² → hypotenuse = √13
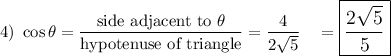
Note: hypotenuse given in problem