Question

A conducting sphere contains positive charge distributed uniformly over its surface. Which statements about the potential due to this sphere are true? All potentials are measured relative to infinity

a. The potential at the center of the sphere is zero.
b.The potential is lowest, but not zero, at the center of the sphere.
c. The potential at the center of the sphere is the same as the potential at the surface.
d. The potential at the center is the same as the potential at infinity.
e. The potential at the surface is higher than the potential at the center.

Answer 1

a. FALSE

b. FALSE

c. TRUTH

d. FALSE

e. FALSE

Step-by-step explanation:

To determine which statements are truth or false you focus in the following formula, for the electric potential generated by a conducting sphere:

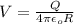`V=(Q)/(4\pi \epsilon_o R)` inside the sphere

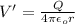`V'=(Q)/(4\pi \epsilon_o r)` for r > R (outside the sphere)

R: radius of the sphere

ε0: dielectric permittivity of vacuum

Q: charge of the sphere

As you can notice, inside the sphere the potential is constant. Inside the sphere, the potential is the same. Outside the surface the potential decreases as 1/r, being r the distance to the center of the sphere.

Hence, you can conclude:

a. The potential at the center of the sphere is zero. FALSE

b.The potential is lowest, but not zero, at the center of the sphere. FALSE

c. The potential at the center of the sphere is the same as the potential at the surface. TRUTH

d. The potential at the center is the same as the potential at infinity. FALSE

e. The potential at the surface is higher than the potential at the center. FALSE