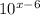Question

Consider the function f(x)= 10^x and the function g(x), which is shown below.

How will the graph of g(x) differ from the graph of f(x)?

g(x)= f(x - 6) = 10^(x-6)

A. The graph of g(x) is the graph of f(x) shifted 6 units elown.
B. The graph of g(x) is the graph of f(x) shifted to the left 6 units.
C. The graph of g(x) is the graph of f(x) shifted 6 units up.
D. The graph of g(x) is the graph of f(x) shifted to the right 6 units.

Answer 1

D. The graph of g(x) is the graph of f(x) shifted to the right 6 units.

Explanation:

Use GeoGebra to graph those two function

f(x) = 10^x

g(x) = 10^(x-6)

Answer 2

B. The graph of g(x) is the graph of f(x) shifted to the left '6' units

Explanation:

Type of transformation change to co-ordinate point

Vertical translation up 'd' units (x ,y) changes to (x , y+d)

Vertical translation down 'd' units (x ,y) changes to (x , y-d)

Horizontal translation left 'c' units (x ,y) changes to (x-c , y)

Horizontal translation Right 'c' units (x ,y) changes to (x+c , y)

Given f(x) translation left 'c' units f(x) changes to f(x-c)

Given f(x) translation right 'c' units f(x) changes to f(x+c)

Given Function f(x) = 10 ˣ

The given graph f(x) translation left '6' units

g(x) = f(x -6) =
`10^(x-6)`

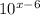
Final answer:-

The graph of g(x) is the graph of f(x) shifted to the left '6' units

g(x) = f(x -6) =
`10^(x-6)`