Answer:
The equation is found to be:
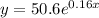
y(20) = 1241.34
Explanation:
The given data is:
x: 3 7 11 14 17
y: 83 142 301 450 722
Now, we find sum summation values, relevant to the formula of exponential regression model, using calculator:
∑ ln y = 27.77305, ∑x ln y = 308.1494, ∑x = 52, ∑ x² = 664
and, n = no. of data points = 5
Now, we use formulae of exponential regression model to find out values of constant:
b = (n∑x lny - ∑x ∑ln y)/[n∑x² - (∑x)²]
b = [(5)(308.1494) - (52)(27.77305)]/[(5)(664) - (52)²]
b = 0.16
Now, for a;
a = (∑ln y - b∑x)/n
Therefore,
a = [(27.77305) - (0.16)(52)]/5
a = 3.9
For, α:
α = e^a = e^3.9
α = 50.6
So, the final equation of exponential regression model is given as:
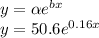
Now, we find value of y for x = 20:
y(20) = (50.6) e^(0.16*20)
y(20) = 1241.34