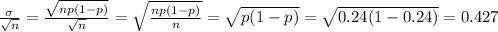Question

Suppose the manager of a restaurant in a commercial building has determined that the proportion of customers who drink tea is 24%. Based on a random sample of 300 customers, what is the standard error for the sampling distribution of the sample proportion of tea drinkers?

Answer 1

0.427

Explanation:

Standard error for the sampling distribution refers to the standard deviation of the samples taken from a population. The standard error equals the standard deviation divided by the square root of the sample size

The probability of customers who drink tea (p) = 24% = 0.24, the sample size of customers (n) = 300.

Standard error =
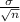`(\sigma)/(√(n) )` where σ is the standard deviation.

`\sigma=√(np(1-p))`

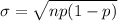
Standard error =
`(\sigma)/(√(n) )= (√(np(1-p)) )/(√(n) ) =\sqrt{(np(1-p))/(n) } =√(p(1-p))=√(0.24(1-0.24)) =0.427`