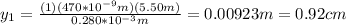Question

Coherent light that contains two wavelengths, 660 nm and 470 nm , passes through two narrow slits with a separation of 0.280 mm and an interference pattern is observed on a screen which is a distance 5.50 m from the slits.

Required:
What is the disatnce on the screen between the first order bright fringe for each wavelength?

Answer 1

λ1 = 0.0129m = 1.29cm

λ2 = 0.00923m = 0.92 cm

Step-by-step explanation:

To find the distance between the first order bright fringe and the central peak, can be calculated by using the following formula:

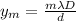`y_m=(m\lambda D)/(d)` (1)

m: order of the bright fringe = 1

λ: wavelength of the light = 660 nm, 470 nm

D: distance from the screen = 5.50 m

d: distance between slits = 0.280mm = 0.280 *10^⁻3 m

ym: height of the m-th fringe

You replace the values of the variables in the equation (1) for each wavelength:

For λ = 660 nm = 660*10^-9 m

`y_1=((1)(660*10^(-9)m)(5.50m))/(0.280*10^(-3)m)=0.0129m=1.29cm`

For λ = 470 nm = 470*10^-9 m

`y_1=((1)(470*10^(-9)m)(5.50m))/(0.280*10^(-3)m)=0.00923m=0.92cm`