Answer:
(A)Show that the ratios StartFraction U V Over X Y EndFraction , StartFraction W U Over Z X EndFraction , and StartFraction W V Over Z Y EndFraction are equivalent.
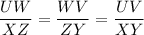
Explanation:
In Triangles WUV and XZY:
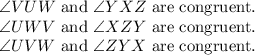
Therefore:

To show that the triangles are similar by the SSS similarity theorem, we have:
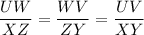
As a check:
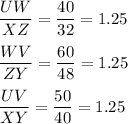
The correct option is A.