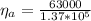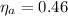Question

An engine draws energy from a hot reservoir with a temperature of 1250 K and exhausts energy into a cold reservoir with a temperature of 322 K. Over the course of one hour, the engine absorbs 1.37 x 105 J from the hot reservoir and exhausts 7.4 x 104 J into the cold reservoir.

1) What is the power output of this engine?

2) What is the maximum (Carnot) efficiency of a heat engine running between these two reservoirs?

3) What is the actual efficiency of this engine?

Answer 1

The power output of this engine is
`P = 17.5 W`

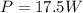
The the maximum (Carnot) efficiency is
`\eta_c = 0.7424`

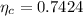
The actual efficiency of this engine is
`\eta _a = 0.46`

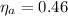
Step-by-step explanation:

From the question we are told that

The temperature of the hot reservoir is
`T_h = 1250 \ K`

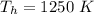
The temperature of the cold reservoir is
`T_c = 322 \ K`

The energy absorbed from the hot reservoir is
`E_h = 1.37 *10^(5) \ J`

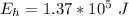
The energy exhausts into cold reservoir is
`E_c = 7.4 *10^(4) J`

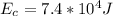
The power output is mathematically represented as

`P = (W)/(t)`

Where t is the time taken which we will assume to be 1 hour = 3600 s

W is the workdone which is mathematically represented as

`W = E_h -E_c`

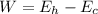
substituting values

`W = 63000 J`

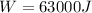
So

`P = (63000)/(3600)`

`P = 17.5 W`

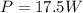
The Carnot efficiency is mathematically represented as

`\eta_c = 1 - (T_c)/(T_h)`

`\eta_c = 1 - (322)/(1250)`

`\eta_c = 0.7424`

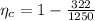
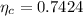
The actual efficiency is mathematically represented as

`\eta _a = (W)/(E_h)`

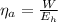
substituting values

`\eta _a = (63000)/(1.37*10^(5))`

`\eta _a = 0.46`