Answer:
Step-by-step explanation:
A circle whose center is
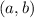 and radius
and radius
 , has equation:
, has equation:
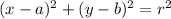
The center of circle is given as origin
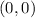 , therefore:
, therefore:

This circle passes
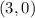 , then the radius of circle is the distance
, then the radius of circle is the distance
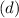 between origin
between origin
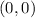 and
and
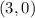
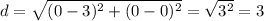
=>
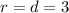
Substitute
 ,
,
 , and
, and
 back into original equation:
back into original equation:
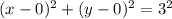
or
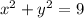
Hope this helps!
:)