Question

A wooden object (conically shaped) has a diameter of 8cm and height of 14cm. It floats in oil with 6cm of its height above oil level. Determine (a)The density of the object (b) If the volume of oil is twice that of the object, what fraction of oil is displaced after immersing the object?

Answer 1

(a) The density of the object is 316/343 × the density of the oil

(b) The fraction of oil displaced after immersing the object is 0.461 of the oil volume

Step-by-step explanation:

(a) The volume, V of a cone of height, h and base diameter, D = 2×r is given by the following equation;

`V = (\pi r^(2) h)/(3)`

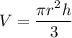
The volume of the object is therefore;

`(\pi * 4^(2) * 14)/(3) = 74\tfrac{2}{3}\pi \, cm^3`

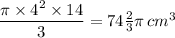
Where 6 cm is above the oil level we have;

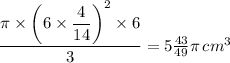`(\pi * \left (6 * (4)/(14) \right )^(2) * 6)/(3) = 5\tfrac{43}{49}\pi \, cm^3` above the oil level

Therefore, volume of the oil displaced =
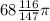`68\tfrac{116}{147}\pi` cm³ = 216.11 cm³

The density of the object is thus;

`\frac{68\tfrac{116}{147}\pi}{ 74\tfrac{2}{3}\pi} * Density \ of \ the \ oil = (316)/(343) \right ) * Density \ of \ the \ oil`

The density of the object = 316/343 × the density of the oil.

(b) The volume of the oil = 2 × Volume of the object =
`2 * 74\tfrac{2}{3}\pi \, cm^3 = 149\tfrac{1}{3}\pi \, cm^3`

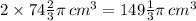
The fraction of the volume displaced, x, after immersing the object is given as follows;

`x = \frac{68\tfrac{116}{147}\pi}{ 149\tfrac{1}{3}\pi} = (158)/(343) = 0.461`

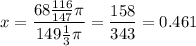
The fraction of oil displaced after immersing the object = 0.461 of the volume of the oil