Answer:
n=10
Explanation:
The given equation is
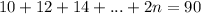 ...(1)
...(1)
Let nth term is 2n.
We need to find the values of n.
It is clear that
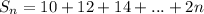 is sum of A.P., whose first term is 10 and common difference is 2.
is sum of A.P., whose first term is 10 and common difference is 2.
Sum of A.P. is
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2021/formulas/mathematics/high-school/nbbqumcy0s5kebc4qw68eqqy1qlvhszlv2.png)
where, a is first term and d is common difference.
Substitute a=10 and d=2 in the above formula.
![S_n=(n)/(2)[2(10)+(n-1)2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/oh8w3pi6pkh0fcnzbiur20ekt4bxg8hmlf.png)
![10+12+14+...+2n=n[10+n-1]](https://img.qammunity.org/2021/formulas/mathematics/high-school/jdzt2sh4vexl8rbjn8tdw4g2bxr2h5gq1i.png)
![10+12+14+...+2n=n[9+n]](https://img.qammunity.org/2021/formulas/mathematics/high-school/wgubm1lhvw6qzchd7pv5wat416szztc1rr.png) ...(2)
...(2)
From (1) and (2), we get
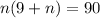

Splitting middle term, we get
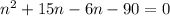
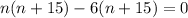
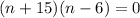
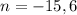
Since, n represents the number of terms so n cannot be a negative number, therefore number of term is 6.
Note: nth term and variable n both are different.

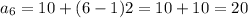
Sixth term is 20. So,
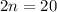

Therefore, the value of n is 10.