Answer:
Here's what I get
Explanation:
Total cost = equipment cost + monthly fee × number of months
Let C = total cost
and e = equipment cost
and f = monthly fee
and x = number of months. Then
C = e + f·x
The condition is that C ≤ $175 or
e + f·x ≤ $175
1. NetGear
e = $99; f = $5/mo
The condition is
99 + 5x ≤ 175
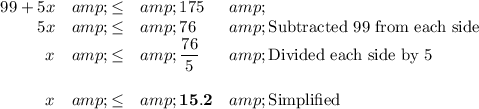
The centre could rent the games for 15 mo.
They would pay $99 for the equipment.
Fifteen months rental at $5/mo = $75.
Total cost = $174.
2. Anytime Games
e = $19; f = $19/mo
The condition is
19 + 19x ≤ 175

The centre could rent the games for eight months.
They would pay $19 for the equipment.
Eight months rental at $19/mo = $152.
Total cost = $171.
3. Recommendation
The Community Centre should rent from NetGear.
They can rent for 15 mo without going over the budget.
With the other company, they can rent for only eight months.
The graphs below show how the costs for the two companies vary with the number of months.
Anything above the horizontal orange line at C = $175 is beyond the Community Centre's budget.