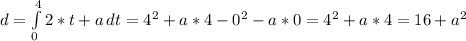Question

Let the velocity of a particle be given by v(t) = 2t+a.(a) Find the number a such that the average value of v(t) on the interval [0,1] is -2.(b) Using v(t) from part (a), find the distance traveled by the particle during the time period from [0,4].

Answer 1

The velocity is v(t) = 2*t + a

a) we want to find the average velocity betwen t = 0 and t = 1.

We can do this as:

Average = (v(1) + v(0))/2 = (2*1 + a + 2*0 + a)/2 = 1 + a

b) now we want to find the total distance traveled in the time lapse from t = 0 to t = 4.

For this we can see the integral:

`d = \int\limits^4_0 {2*t + a} \, dt = 4^2 + a*4 - 0^2 - a*0 = 4^2 + a*4 = 16 + a^2`