Question

A horizontal line contains points A, C, B. 2 lines extend from point C. A line extends to point E and another line extends to point D. An arc represents angle A C D.

Ray CE is the angle bisector of AngleACD. Which statement about the figure must be true?

mAngleECD = One-halfmAngleECB
mAngleACE = one-halfmAngleACD
AngleACE Is-congruent-to AngleDCB
AngleECDIs-congruent-to AngleACD

Answer 1

b

Explanation:

took test

Answer 2

Option (2).

Explanation:

In the figure attached,

A, C and B are the points lying on a straight line.

2 lines EC and DC have been drawn by extending the lines from C to E and D respectively.

Ray CE is the angle bisector of ∠ACD.

That means CE divides ∠ACD in two equal parts.

m∠ACE = m∠DCE

Since m∠ACD = m∠ACE + m∠DCE

= 2(m∠ACE)

m∠ACE =
`(1)/(2)(\angle ACD)`

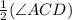
Therefore, option (2) will be the answer.