Question

When y is 4, p is 0. 5, and m is 2, x is 2. If x varies directly with the product of p and m and inversely with y, which equation models the situation?

x p m y = 8
StartFraction x y Over p m EndFraction = 8
StartFraction x p m Over y EndFraction = 0. 5
StartFraction x Over p m y EndFraction = 0. 5

Answer 1

B

Explanation:

Answer 2

`(xy)/(pm)=8`

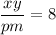
Explanation:

If x varies directly as the product of p and m, and inversely with y, the relation can be written ...

x = k(pm)/y . . . . where k is the constant of proportionality

__

This can be solved for k:

k = xy/pm

For the given values, the value of k is ...

k = (2)(4)/((0.5)(2)) = 8

Then the relation between the variables can be written ...

(xy)/(pm) = 8