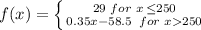Answer:
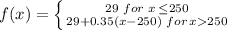
Explanation:
If we call "x" the number of call minutes used with this plan, the piecewise function used to describe it must represent;
a) a constant value of 29 for any x value smaller than or equal to 250
b) a line with positive slope of 0.35 for the region with x larger than 250. The mathematical representation of such increasing straight line, should be given by a line of slope m = 0.35, and containing the point (250, 29) which is the starting point for this right hand side portion of the domain:
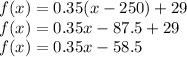
So the function should look like:
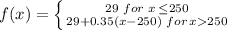
or as shown above, in a more simplified form: