Question

A cylindrical container with a radius of 6 cm and a height of 10 cm is filled with water to a depth of 6 cm. A sphere with a radius of 3 cm is placed at the bottom of the container. a) What is the volume of the water to the nearest tenth? b) What is the volume of the sphere to the nearest tenth? c) How much higher does the water level rise in the container, to the nearest tenth, after the sphere is placed inside?

Answer 1

a) The volume of the water is approximately 678.6 cm³.

b) The volume of the sphere is approximately 113.1 cm³.

c) The new height of the water is approximately 7 cm, one cm higher than before.

Explanation:

To solve this problem we first need to calculate the volume of the water, which is given by the cylinder volume, since it's stored in a cylindrical container.

`\text{water volume} = \pi*r^2*h\\\text{water volume} = \pi*(6)^2*6\\\text{water volume} = \pi*36*6\\\text{water volume} = 678.584 \text{ }cm^3\\`

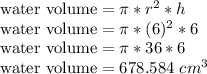
We now need to calculate the volume of the sphere, by using the appropriate formula:

`\text{volume sphere} = (4)/(3)\pi*r^3\\\text{volume sphere} = (4)/(3)\pi*(3^3)\\\text{volume sphere} = (4)/(3)\pi*27\\\text{volume sphere} = 113.09 \text{ } cm^3`

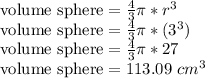
When the sphere is inserted into the cylinder the volume of the things that are inside of the container are added up, so the volume would be the volume of the water plus the volume of the sphere, we can use this information to calculate the height of the water as shown below:

`\text{total volume} = \text{water volume} + \text{sphere volume}\\\text{total volume} = 678.6 + 113.1 = 791.7\\\text{total volume} = \pi*r^2*h_(new)\\791.7 = \pi*(6)^2*h_(new)\\h_(new) = (791.7)/(\pi*36) = 7.00016\text{ } cm`

a) The volume of the water is approximately 678.6 cm³.

b) The volume of the sphere is approximately 113.1 cm³.

c) The new height of the water is approximately 7 cm, one cm higher than before.