By applying the law of sine, the magnitude of both angles B and B', which solve this ambiguous case include; A. B = 64.13⁰ or B' = 115.87⁰
In order to determine the magnitude of both angles B and B', we would apply the law of sine:
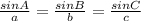
Substituting the parameters into the formula above, we have;
sinB'/16 = sin60/15.4
sinB'/16 = 0.8660/15.4
sinB'/16 = 0.0562
sinB' = 0.0562 × 16
B' =
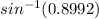
B' = 115.87°.
Now, we can determine the magnitude of angle B by using the formula for supplementary angles:
B + B' = 180
B + 115.87 = 180
B = 180 - 115.87
B = 64.13°.
Complete Question:
In the following triangle, θ = 60. find the values of the angles B and B', which solve this ambiguous case