Question

If the terminal ray of β lies in the fourth quadrant and sin (β) = -√3/3 determine cos(β) in simplest form.

I really appreciate your help, please help.
Thank you
God bless

Answer 1

cos(β) = √6/3

Explanation:

Given β lies in the fourth quadrant and sin (β) = -√3/3

we know that the trigonometry formula

sin²(β)+cos²(β) = 1

cos²(β) = 1- sin²(β)

cos²(β) = 1- ( -√3/3)²

=
`1-(3)/(9) } } =(6)/(9)`

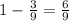
cos(β) = √6/9 = √6/3

we Know that β lies in the fourth quadrant so cos(β) is Positive

cos(β) = √6/3