Question

A company's total sales (in millions of dollars) t months from now are given by S(t) = sqrt t + 2. In your own words, find and interpret S(20) and S'(20). Use these results to estimate the total sales after 24 months and after 25 months.

Answer 1

S(20) =
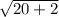`√(20+2)` = 4.69 ; value of total sales after 20 months is 4.69 million dollars

S'(20) =
`(1)/(√(20+2) )` = 0.21 ; increase in the total sales after 20 months is 0.21 millions of dollars

S(24) =
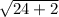`√(24+2)` = 5.10; 5.10 millions of dollars

S(25) =
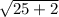`√(25+2)` = 5.20 ; 5.20 millions of dollars

Explanation:

`S(t) = √(t+2)`

`S(t+h) = √(t+2+h)`

`S(t+h) - S(t)= √(t+2+h )- √(t+2)`

`(S(t+h) - S(t))/(h)= (√(t+2+h )- √(t+2))/(h)`

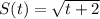
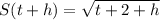
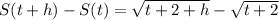
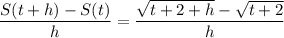
By rationalization:

`(√(t+2+h )- √(t+2))/(h) * \frac{ {√(t+2+h )- √(t+2)} }{ {√(t+2+h )- √(t+2)}}`

`\\ \\ (t+2+h-t-2)/(h √(t+2+h )+ √(t+2) ) = \frac {h}{√(t+2+h )+√(t+2) }`

=
`\frac {1}{√(t+2+h )+√(t+2) }`

`\lim_(k \to \infty) \frac {1}{√(t+2+h )+√(t+2) } = (1)/(t+2)`

`S' (t) = (1)/(√(t+2) )`

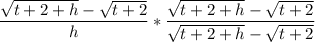
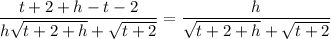
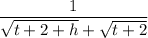
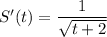
S(20) =
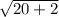`√(20+2)` = 4.69 ; value of total sales after 20 months is 4.69 million dollars

S'(20) =
`(1)/(√(20+2) )` = 0.21 ; increase in the total sales after 20 months is 0.21 millions of dollars

S(24) =
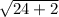`√(24+2)` = 5.10; 5.10 millions of dollars

S(25) =
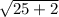`√(25+2)` = 5.20 ; 5.20 millions of dollars