Answer:
P(X≥112) = 0.9495
The percentage of the games that Easton bowls does he score higher than 112 = 94.95%
Explanation:
Given mean of the Population = 130
Given standard deviation of the Population = 11
Let X= 112
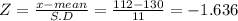
P(X≥112) = P(Z≥ z)
= 1-P(Z≤z)
= 1- ( P(Z≤-1.636)
= 1- (0.5-A(-1.636)
= 0.5 +A(1.636)
= 0.5 + 0.4495
P(X≥112) = 0.9495
The percentage of the games that Easton bowls does
he score higher than 112 = 94.95%