Question

A potato was launched in the air using a potato gun. The function for the situation was h(t)=-16t^2 +100t+10, where t was the time in seconds and h is the height in ft. What was the maximum height? What was the lowest height of the potato? What was the lowest times that applies to the actual situation? What is the greatest time that applied to the situation? What are the domain and range of the function using set builder notation?

Answer 1

The height equation is:

h(t)=-16t^2 +100t+10

A) To find the maximum height, we must find the time where the velocity is 0, so we must derive it with respect to the time.

v(t) = -2*16*t + 100 = 0

t = 100/(2*16) = 3.125s

Now we put this time in our height equation:

h(3.125s) = -16*3.125^2 + 100*3.125 + 10 = 166.25 ft.

B) The lowest heigth of the potato will be h = 0ft, when the potato hits the ground.

C) the lowest time that works for that function is t = 0s, when the potato is fired by the gun.

D) the maximum time can be finded when the potato hits the ground, afther that point the equation does not work anymore, let's find it,

h(t) = 0 = -16t^2 +100t+10

we can solve it using Bhaskara's equation:

`t = (-100 +- √(100^2 +4*16*10) )/(-2*16) = (-100 +- 103.2)/(-32)`

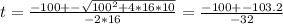
So the two solutions are:

t = 6.3s

t = -0.1s

We need to chose the positive time, as we already discused that the minimum time that works for the equation is t = 0s.

so here the answer is t = 6.3s

E) the domain is 0s ≤ t ≤ 6.3s

The range is 0ft ≤ h ≤ 166.25 ft.