Question

Given: w ∥ x and y is a transversal. Prove: ∠3 and ∠5 are supplementary. Parallel and diagonal lines w and x are cut by horizontal transversal y. On line w where it intersects with line y, 4 angles are created. Labeled clockwise, from uppercase left, the angles are: 1, 3, 4, 2. On line x where it intersects with line y, 4 angles are created. Labeled clockwise, from uppercase left, the angles are: 5, 7, 8, 6. Use the drop-down menus to complete the proof. Given that w ∥ x and y is a transversal, we know that ∠1 ≅∠5 by the . Therefore, m∠1 = m ∠5 by the definition of congruent. We also know that, by definition, ∠3 and ∠1 are a linear pair so they are supplementary by the . By the , m∠3 + m ∠1 = 180. Now we can substitute m∠5 for m∠1 to get m∠3 + m∠5 = 180. Therefore, by the definition of supplementary angles, ∠3 and ∠5 are supplementary.

Answer 1

1. Corresponding angles theorem

2. Linear pair postulate

3. Definition of supplementary angles

Answer 2

1.Corresponding angles theorem

2.Linear postulate

3.By the definition of supplementary angles

Explanation:

We are given that

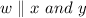`w\parallel x \ and \ y` is a transversal.

We have to prove
`\angle 3` and
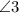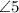`\angle 5` are supplementary

Proof:

1.Given that
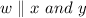`w\parallel x \ and \ y` is a transversal.

We know that
`\angle 1\cong \angle 5`

Reason:Corresponding angles theorem

Therefore,
`m\angle 1=m\angle 5`

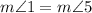
by the definition of congruent.We also know that, by definition, angle 3 and angle 1 are a linear pair.

Therefore, they are supplementary by linear pair postulate

By the definition of supplementary angles

`m\angle 3+m\angle 1=180^(\circ)`

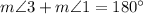
Now, we can substitute
`m\angle 5=m\angle 1`

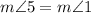
Then, we get

`\m\angle 3+m\angle 5=180^(\circ)`

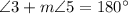
Therefore, by the definition of supplementary angles,angle 3 and angle 5 are supplementary