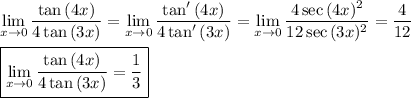Question

Evaluate the limit of tan 4x/ 4tan3x​

Answer 1

1/3

Explanation:

The ratio is undefined at x=0, so we presume that's where we're interested in the limit. Both numerator and denominator are zero at x=0, so L'Hôpital's rule applies. According to that rule, we replace numerator and denominator with their respective derivatives.

`\displaystyle\lim\limits_(x\to 0)(tan((4x)))/(4tan((3x)))=\lim\limits_(x\to 0)\frac{\tan'{(4x)}}{4\tan'{(3x)}}=\lim\limits_(x\to 0)\frac{4\sec{(4x)^2}}{12\sec{(3x)^2}}=(4)/(12)\\\\\boxed{\lim\limits_(x\to 0)(tan((4x)))/(4tan((3x)))=(1)/(3)}`