Question

What type of conic section is given by the equation y^2-9x^2=900 and what is the domain and range? Show your work.

Answer 1

Domain : x ∈ Real Numbers

Range : y ≥ 30

Explanation:

The given equation is:

`y^2-9x^2=900`

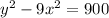
Simplifying it

`(y^2)/(900)-(9x^2)/(900)=(900)/(900)\\(y^2)/(900)-(x^2)/(100)=1\\(y^2)/(30^2)-(x^2)/(10^2)=1`

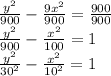
Where Standard equation of parabola is:

`(y^2)/(a^2)-(x^2)/(b^2)=1`

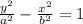
Which are similar. Conic Section is a parabola.

Find Domain and Range:

Simplify the given equation:

`y^2-9x^2=900\\y=√(9x^2+900),y=-√(9x^2+900)\\y=3√(x^2+100),y=-3√(x^2+100)`

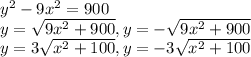
For whatever value of x, term under the square root always remains positive, so

Domain : x ∈ Real Numbers

For minimum value of x i.e 0, y=30. If we increase x, y also increases. So

Range : y ≥ 30