Question

What is the gravitational force between mars and Phobos

Answer 1

`F=5.16* 10^(15)\ N`

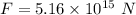
Step-by-step explanation:

We have,

Mass of Mars is,
`m_M=6.42* 10^(23)\ kg`

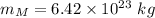
Mass of its moon Phobos,
`m_P=1.06* 10^(16)\ kg`

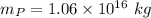
Distance between Mars and Phobos, d = 9378 km

It is required to find the gravitational force between Mars and Phobos. The force between two masses is given by

`F=G(m_Mm_P)/(d^2)`

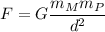
Plugging all values, we get :

`F=6.67* 10^(-11)* (6.42* 10^(23)* 1.06* 10^(16))/((9378* 10^3)^2)\\\\F=5.16* 10^(15)\ N`

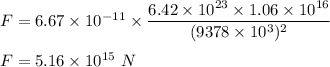
So, the gravitational force is
`5.16* 10^(15)\ N`.