In the given circle with
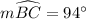 , applying the chord-tangent angle theorem yields
, applying the chord-tangent angle theorem yields
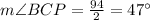 , as the angle is half the intercepted arc.
, as the angle is half the intercepted arc.
In the circle,
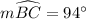 .
.
Theorem Application:
Apply the theorem that states, "An angle formed by a chord and a tangent that intersect on a circle is half the measure of the intercepted arc."
Interpreting the Theorem:
In this context, the chord is
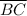 , and the tangent is
, and the tangent is
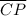 . The angle formed at B by this chord and tangent is
. The angle formed at B by this chord and tangent is
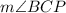 .
.
Finding the Measure of
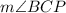 :
:
According to the theorem,
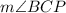 is half the measure of the intercepted arc, which is
is half the measure of the intercepted arc, which is
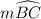 .
.
Calculation:
![\[m\angle BCP = \frac{m\widehat{BC}}{2} = (94)/(2) = 47^\circ\]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/o63yo6hm3vy0x8n9h5lv5ixhycbwmu152l.png)
Therefore, the measure of
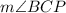 is
is
 , half of
, half of
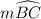 .
.
The complete question is:
In the circle,
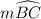 =94°. The diagram is not drawn to scale. What is
=94°. The diagram is not drawn to scale. What is
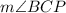 ?
?