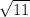Answer:
Axis of symmetry is x = -2
(-2, -11) is the vertex
Roots are
-2 +
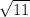 , -2 -
, -2 -
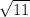
Explanation:
a) Axis of symmetry equation is: x = -b/2a
Original equation: y =
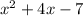
So...
x= -4/2(1) = -2
Axis of symmetry is x = -2
b) Vertex Point can be found by plugging into original equation.
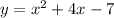
=> y =
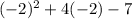
=> 4 - 8 - 7 = y
=> -11 = y
(-2, -11) is the vertex
c) quadratic formula is
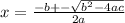
Lets plug in the values.
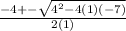
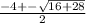
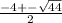

-4 +- 2
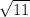
--------------
2
Here, i will factor out 2, and take out the +- and make it into two equations
2(-2 +
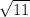 ) / 2 = -2 +
) / 2 = -2 +
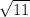
2(-2 -
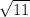 ) / 2 = -2 -
) / 2 = -2 -
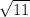
x= -2 +
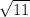
or
x = -2 -
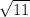
Roots are
-2 +
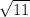 , -2 -
, -2 -