Question

In triangle ABC points M and N lie on sides AB and BC, respectively such that MN∥ AC . Segments AN and CM intersect at point K and AK = KC. Prove that △ABC is isosceles.

Answer 1

Explanation:

An isosceles triangle has two equal sides and two equal base angles.

Given that : AK = KC and MN∥ AC

ΔMNB is similar to ΔACB (congruence property)

ΔANB = ΔANC (SAS congruence property)

ΔCMB = ΔCMA (SAS congruence property)

`(AB)/(BN)` =
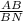`(AC)/(CN)` (Angle bisector theorem)

So that:

<BAC = <ACB (base angle property of an isosceles triangle)

/AB/ = /BC/ (side property of an isosceles triangle)

Therefore, ΔABC is an isosceles triangle.